Gaeune's Blog-[programmers] 스티커 모으기(2)

문제

문제점 해결

해당 문제는 DP를 사용해 해결할 수 있는 문제이다. 문제는 원형이지만 한 곳을 끊는 다면 배열과 같은 모양이 된다. sticker 길이와 같은 DP배열 2개를 만들고 0번 인덱스를 선택 하는 경우와 선택하지 않는 경우일 때의 값을 계산해 결과를 도출한다.

예제 문제를 살짝 변형해서 입력이 [14, 6, 5, 11, 12, 9, 2, 10]로 들어올 때의 최댓값을 구해보자.

0번 인덱스를 선택하는 경우

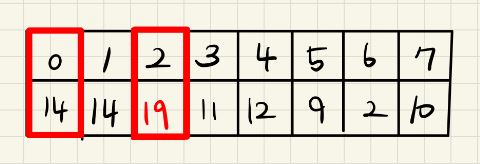
0번 인덱스를 선택한다면 1번 인덱스는 건너뛰고 2번 인덱스를 선택하기 때문에 0번 인덱스 선택하는 경우(dp1 배열)엔 dp1배열 0번 값과 1번 값에 sticker배열 0번 인덱스 값을 저장해준다.

dp1[0] = sticker[0];
dp1[1] = sticker[0];

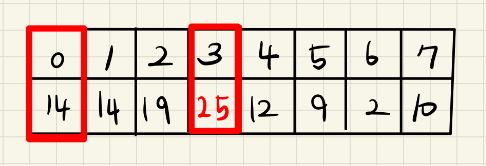
이미 선택한 0번 인덱스와 2번 인덱스를 더했을 때의 값과 1번 인덱스를 비교해 최댓값을 선택한다.

0번 + 2번 < 3번 이므로 선택을 0번과 3번으로 바꿔준다.

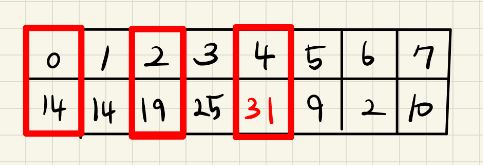
0번 + 3번 < 0번 + 2번 + 4번 이므로 선택을 바꿔준다.

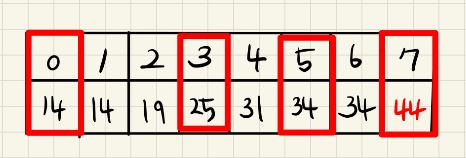
이 과정을 반복하면 아래와 같은 결과가 나온다.

풀이

class Solution {
	public int solution(int sticker[]) {
		int answer = 0;
        
        if(sticker.length < 3) {
			for (int i = 0; i < sticker.length; i++) {
				answer = Math.max(sticker[i], answer);
			}
			
			return answer;
		}

		int[] dp1 = new int[sticker.length];
		int[] dp2 = new int[sticker.length];

		dp1[0] = sticker[0];
		dp1[1] = sticker[0];
		for (int i = 2; i < sticker.length - 1; i++) {
			dp1[i] = Math.max(sticker[i] + dp1[i - 2], dp1[i - 1]);
		}

		dp2[1] = sticker[1];
		for (int i = 2; i < sticker.length; i++) {
			dp2[i] = Math.max(sticker[i] + dp2[i - 2], dp2[i - 1]);
		}

		int max = 0;
		for (int i = 0; i < sticker.length; i++) {
			max = Math.max(dp1[i], dp2[i]);
			answer = Math.max(answer, max);
		}
		
		return answer;
	}
}

참고로 길이가 33번 케이스의 sticker 배열 길이가 1또는 2로 추측되므로 if문을 넣지 않으면 런타임에러가 발생하니 제한 사항을 꼭 확인해줘야 한다.